Big Features

I implemented the following features related to the Volumetric Path Tracer in Nori:

The relevant files related to the volumetric path tracer are the following:

/src/integrators/volpath.cpp
/include/nori/medium.h
/include/nori/phase.h
/include/nori/accel.h

Note that I also added the direct lighting and furnace tests to the continuous integrations for the volumetric path tracer integrator.

Henyey-Greenstein Phase Function

I implemented the Henyey-Greenstein phase function for homogeneous and heterogeneous medias even if I finally only used the isomorphic equivalent case.
The source files of interest are the following:

/src/phases/hg.cpp

Chi Square Warp Test — The passing Chi² Warp Test

Homogeneous Media

As I wanted to render smoke I first had to implement the homogeneous case before the heterogeneous one. My implementation is based on PBRT's implementation but also includes some logic from Mitsuba like the

struct MediumQueryRecord

and the

struct PhaseFunctionQueryRecord

The source files of interest are the following:

/src/mediums/homogeneous.cpp

SigmaS: rgb(1.0,1.0,1.0) SigmaA: rgb(0.0,0.0,0.0)

SigmaS: (0.0,0.0,0.0) SigmaA: (1.0,1.0,1.0)

SigmaS: (0.8 0.2 0.8) SigmaA: (0.2 0.8 0.2)

Heterogenous Media

Once the homogeneous was implemented there were actually two main steps: Implement the heteregenous media in Nori and maybe the harder part, getting the data which we want to render.
The source files of interest are the following:

/scripts/smokeDataExtractor.py
/scripts/pointcache.c
/include/nori/voxelgrid.cpp

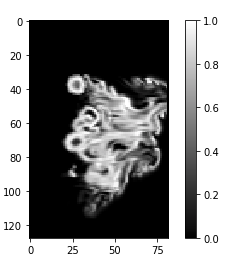
I will begin by the end and explain how I actually got the data for the heteregenous media To run the script, first replace the pointcache.c file in Blender's source code with my modified one and then recompile it. Then just run any smoke simulation you want in Blender and run

python3 smokeDataExtractor.py path/to/smokeSimulationData

from which you will get two output files called

path/to/smokeSimulationData.density

and

path/to/smokeSimulationData.albedo

which you can then use in Nori.

You can freely download my script here.

Smoke in Blender — A 2D cut from the parsed smoke data

To implement the heteregenous media I used a technique called Woodcock Tracking which in other words simplifies the problem of the heterogenous medias to the homogeneous case and has the advantage of beeing an unbiased technique compared to Ray Marching for example. The problem with the heterogenous case is that the absorption and the scattering coefficient are no more homogeneous. A "brute-force" way would be to seperate our volume in piecewise homogeneous volumes but this technique is rather inefficient especially if there are many medium boundaries. A smarter and more efficient way is to simulate a homogeneous media by adding a fictious medium which fills the volume bounds in a way that the whole volume can be seen as a homogeneous media. (Images from Eurographics 2018 slides about Monte Carlo Sampling in Volumetric Media, Jan Novak)

Delta-Tracking — Stochastic sampling to estimate free path

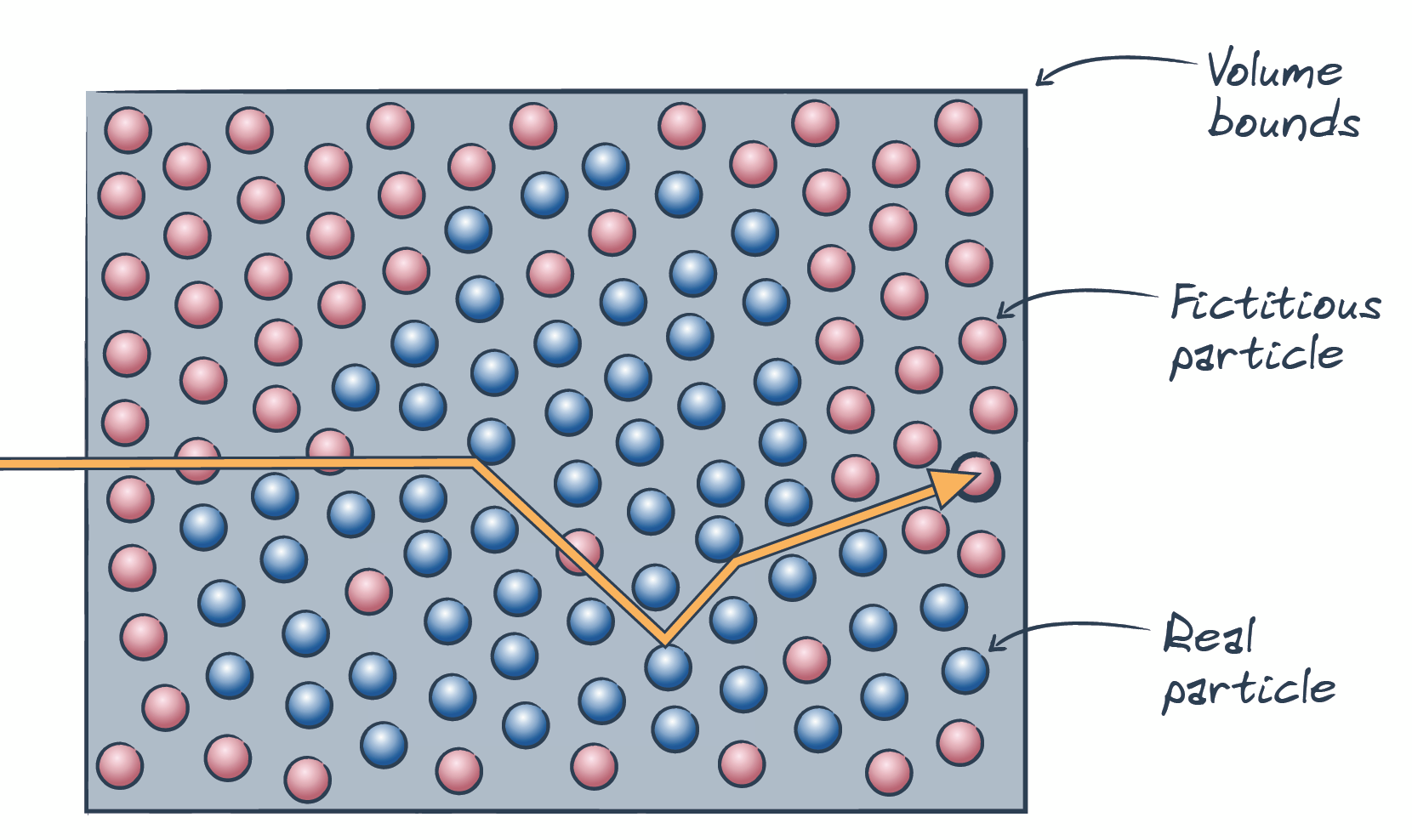
We can then estimate the distance travelled by the light until a real collision occurs using stochastic sampling so that we can sample a distance and check if there is a collision with a real particle or a fictious particle in which case we continue and sample a new distance which we add to the already sampled distance. Alternatively from using the albedo grid from the simulation we can also set the albedo to a constant value returning to the homogeneous case but preserving the custom shape of the volume.

Volume with 0.2 albedo — Volume rendered with a constant albedo of 0.2

Volume with 0.8 albedo — Volume rendered with a constant albedo of 0.8

Realistic Cloud — A more realistic looking cloud with an overall lower density rendered at 1024 samples per pixel

Funny Stuff